Les déchirures : I. feuilles adhésives

Support plan

Bien que les papiers peints ne soient plus très à la mode, on s’est tous au moins une fois risqué à détapisser un mur. Pour ce faire, on décolle une partie du papier sur laquelle on tire en espérant détacher un lambeau le plus long possible afin que le travail se termine rapidement. Cependant, on constate très vite combien cette activité est frustrante car bien souvent le lambeau adopte une forme triangulaire au lieu de conserver une forme rectangulaire comme on le souhaiterait. On ne parvient donc pas à retirer en une seule opération autant de papier peint qu’on le voudrait. L’énervement suscité par cet effet pervers nous incite à tirer plus violemment sur les lambeaux mais en vain car la longueur des morceaux n’en est que réduite!

La forme des lambeaux, bien qu’approximativement triangulaire, n’est pas très régulière. Cela provient de plusieurs facteurs. L’adhésion et la vitesse avec laquelle on tire sur le lambeau ne sont généralement pas uniformes. L’angle que fait le lambeau avec le mur varie aussi lors de l’opération. Enfin, une torsion est souvent appliquée au lambeau lors du détachement. Tous ces facteurs influencent la forme des déchirures.

Une expérience un peu plus contrôlée peut facilement être réalisée chez soi à l’aide d’un morceau d’adhésif. Comme illustré sur la figure ci-dessous :

1. Prenez de l’adhésif de 5cm de large et coupez une bande d’une longueur d’environ 15cm. Collez cette dernière sur une table en laissant dépasser 3-4cm d’adhésif.
2. Faites ensuite deux incisions parallèles dans la partie de l’adhésif qui n’adhère pas à la table. Ces incisions se situeront à 0.5cm des bords latéraux et iront du bord libre de l’adhésif jusque la table. La partie non collée de l’adhésif est donc maintenant constituée de 3 languettes : une au centre d’une largeur de 4cm et deux autres externes d’une largeur de 0.5cm.
3. Rabattez les deux languettes externes pour les coller sur la tranche de la table. De cette manière, la seule partie qui n’adhère pas à la table est la languette centrale large de 4cm. Votre dispositif expérimental est maintenant prêt à être utilisé.
4. Tirez doucement sur la languette centrale pour la décoller. De façon à garder un angle constant entre la languette et la table, faites cette opération avec une angle de 180 degrés. C’est-à-dire en rabattant la languette de telle manière que sa face non adhésive soit constamment parallèle avec la table.
5. A mesure que la languette se décolle, vous constaterez que les deux fissures initiées par les deux incisions se rapprochent. La surface de la languette en contact avec la table diminuant au cours du processus, il est donc de plus en plus aisé de la décoller. Afin de garder une vitesse constante pour l’avancée du front de décollement, il convient alors de tirer de moins en moins fort. Quand les deux fissures se sont rejointes, la languette de forme triangulaire se détache de son support.

L’angle que fait chaque fissure avec la direction le long de laquelle on tire est noté (ce qui conduit à un angle au sommet du triangle valant ). L’expression de cet angle en fonction des paramètres du système vaut [1,2]

où est l’épaisseur de l’adhésif (typiquement 50 µm), est l’angle de “peeling” mesuré en radian ( dans cette expérience), c’est-à-dire l’angle avec lequel on détache la languette adhésive, est le module de flexion de la feuille adhésive ( étant le module de Young du matériau composant la feuille), est l’énergie d’adhésion par unité de surface et est l’énergie de fracture par unité de surface.

Plus est grand plus la longueur de la languette détachée sera petite pour une largeur donnée (et plus frustrant sera le détapissage). La relation ci-dessus nous informe que plus l’adhésion est grande plus sera grand, ce qui est assez intuitif. Elle nous informe également que plus l’épaisseur est grande plus sera grand également, ce qui est moins intuitif. Il faut donc éviter de tapisser sur un papier peint déjà posé si on ne veut pas se compliquer la tâche lors d’un détapissage à venir. Finalement, plus le papier peint se déchire facilement (plus est faible) plus sera grand aussi, ce qui est assez intuitif. Il vaut donc mieux utiliser un papier de bonne qualité qui ne se déchirera pas trop aisément.

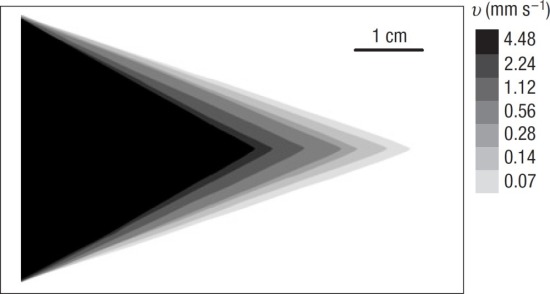
Un dernier paramètre sur lequel on peut jouer est la vitesse à laquelle on décolle l’adhésif. L’énergie d’adhésion augmente généralement avec cette vitesse et conduit donc à une valeur de plus grande. La figure ci-dessous [1] illustre cette propriété en montrant que la longueur diminue lorsque la vitesse augmente. Il faut donc tirer le plus doucement possible afin de diminuer la valeur de et obtenir des longueurs de lambeau les plus grandes possibles.

Interprétation physique.

On peut comprendre assez facilement l’existence d’un angle optimal apparaissant lors de la déchirure d’une feuille adhésive. L’énergie injectée dans le système provient du travail de la force exercée sur la languette (le lambeau) lorsqu’on tire pour la détacher. Imaginons que la force appliquée sur la languette est initialement nulle et augmente progressivement. Il est clair, après avoir réalisé l’expérience décrite ci-dessus, que si la force exercée est trop faible le front de décollement reste immobile (la languette ne se décolle pas et ne se fissure donc pas non plus). Il existe donc une force minimale à appliquer pour commencer à décoller et fissurer la languette. C’est-à-dire qu’il existe une énergie minimale à injecter dans le système, si on considère un déplacement infinitésimal donné, pour déchirer la languette.

Cette énergie injectée se répartit en énergie de fracture, en énergie d’adhésion, puisqu’il faut fissurer et décoller l’adhésif, mais aussi en énergie élastique puisque la languette est courbée quand on la tire (il y a pli qui relie par la partie collée de l’adhésif à la languette sur laquelle on tire). La somme de ces trois énergies constitue l’énergie totale du système. Pour trouver la trajectoire suivie par chaque fissure, il convient donc de minimiser cette énergie totale. Dès que l’énergie injectée sera égale à ce minimum, le front de décollement pourra avancer suivant l’angle correspondant à ce minimum d’énergie.

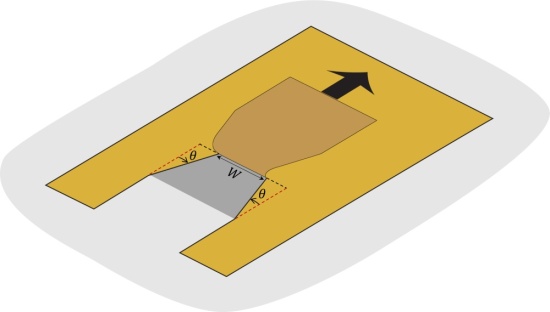
Sur le schéma ci-dessous, on constate que :

1. La longueur de la fissure sera la plus courte si celle-ci avance avec un angle représentée par les pointillés rouge. Toute autre trajectoire linéaire possédant un angle conduit à une longueur de fissure plus grande et donc à une énergie plus grande à dépenser. L’énergie de fracture favorise donc un angle nul.
2. La surface décollée, représentée par le trapèze gris, est quant à elle la plus grande possible pour (on a dans ce cas un rectangle). Pour minimiser la surface à décoller, et donc minimiser l’énergie nécessaire pour décoller la languette, il faut au contraire un angle qui tend vers .
3. La courbure du pli est quant à elle constante tout au long du processus mais l’énergie élastique du pli augmente non seulement avec cette courbure (elle augmente comme le carré de celle-ci) mais aussi avec la largeur du pli. Cette largeur diminue d’autant plus vite avec l’avancée du front de décollement que tend vers .

On a donc trois termes énergétiques, dont deux favorisent et un qui favorise . Le système doit donc trouver un compromis afin de qu’aucun des trois termes ne soit complètement défavorisé. Il choisira donc un angle strictement positif mais aussi strictement inférieur à . La valeur précise de cet angle dépend de la pondération de ces trois termes énergétiques [3].

Par exemple, si le matériau composant la languette est très difficile à fissurer ( très grand), et que l’adhésif adhère peu et qu’il se courbe facilement alors l’énergie totale est dominée par l’énergie de fracture. Dans ce cas, minimiser l’énergie totale revient essentiellement à minimiser l’énergie de fracture. Il faut donc que . C’est bien ce que nous dit l’expression de écrite plus haut.

Pour conclure, on constate que l’expression de est indépendante de la largeur . Ce qui signifie que chaque fissure ce propage avec un angle constant jusqu’à ce qu’elles se rejoignent. Elles se propagent donc en ligne droite et dessine un triangle. Même si la valeur de peut varier d’un système à l’autre, suivant les valeurs de paramètres , , et , la forme triangulaire est une caractéristique robuste commune à tous les systèmes. On peut donc se demander s’il n’existe pas un moyen d’influer sur la direction des trajectoires des fissures pour obtenir d’autres figures géométriques. Nous verrons dans un prochain article que si l’adhésif est posé sur un support courbe, les trajectoires ne sont plus rectilignes et qu’elles peuvent même s’éloigner l’une de l’autre.

Pour une vision artistique des choses : Jacques Villeglé.

1. E. Hamm, P. Reis, M. Leblanc, B. Roman et E. Cerda, Nature Mater. 7, 386 (2008)
2. O. Kruglova, F. Brau, D. Villers et P. Damman, Phys. Rev. Lett. 107, 164303 (2011)
3. On retrouve ici un raisonnement similaire à celui rencontré dans l’article sur les structures hiérarchiques de plis dans les rideaux où la longueur de fusion de deux plis était déterminée par deux termes énergétiques, l’un favorisant les grandes valeurs de () et l’autre favorisant les petites valeurs de (). Le système devait alors choisir une valeur de intermédiaire afin de minimiser l’énergie totale égale à la somme de ces deux énergies (voir le graphique suivant).