Les déchirures : II. Feuilles adhésives

 

Support courbe

Comme nous l’avons vu dans l’article précédent, la forme d’un lambeau détaché d’un film mince adhésif est invariablement triangulaire limitant ainsi sa longueur . Si sa largeur initiale vaut , sa longueur sera avec

où est l’épaisseur de l’adhésif, est l’angle de “peeling” mesuré en radian, c’est-à-dire l’angle avec lequel on détache la languette adhésive, est le module de flexion de la feuille adhésive ( étant le module de Young du matériau composant la feuille), est l’énergie d’adhésion par unité de surface et est l’énergie de fracture par unité de surface.

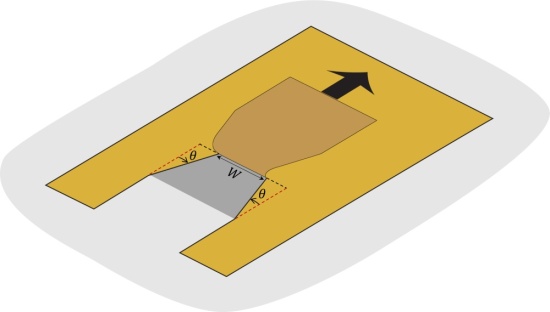
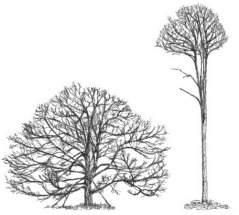
Cependant, la forme d’un lambeau n’est invariablement triangulaire que si le film mince est collé sur un support plan. Si le support est courbe d’autres formes de lambeau peuvent être obtenues. Comme illustré sur la figure ci-dessus :

1. Prenez, par exemple, un tuyau d’évacuation d’eau en plastique ayant un diamètre valant cm et ayant une longueur d’environ 10 cm. Coupez le en deux dans le sens de la longueur de façon à obtenir deux demi coques cylindriques (cette opération sera réalisée par un adulte avec un outil rotatif de type Dremel, attention de ne pas se couper!).
2. Collez un adhésif sur l’une des demi-coques cylindriques et faites y deux incisions parallèles de quelques centimètres de long (ligne rouge) et séparées d’une distance .
3. Détachez la partie ainsi libérée de l’adhésif et tenez-la de façon à ce que le lambeau forme un angle avec le support.
4. Si les opérations 2 et 3 ont été réalisées sur l’intérieur de la demi-coque cylindrique, on observe que le front de décollement est incurvé dans la direction du déplacement (pointillés rouges).
5. Si les opérations 2 et 3 ont été réalisées sur l’extérieur de la demi-coque cylindrique, on observe que le front de décollement est incurvé dans la direction opposée au déplacement (pointillés rouges).

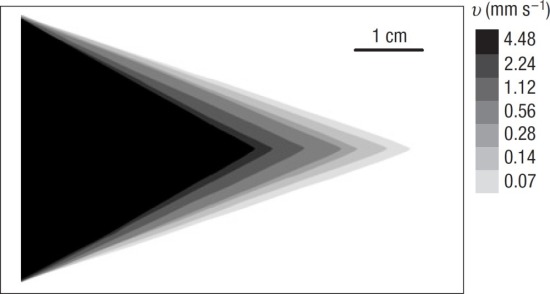
Suivant que l’adhésif se trouve sur l’intérieur ou l’extérieur du cylindre, la forme du front de décollement est différente. On a donc une brisure de symétrie qui se traduit dans les formes de lambeau obtenues. En effet, si maintenant vous tirez sur le lambeau en essayant de garder un angle constant et une vitesse constante du front de décollement, on obtient les formes montrées dans la figure ci-dessous.

1. Forme triangulaire de lambeau obtenue sur un support plan.
2. Forme acuminée obtenue en détachant le lambeau de la surface extérieure du cylindre (, voir ci-après). La convergence des deux fissures est accélérée conduisant à un lambeau de plus faible longueur (comparé à un support plan) pour une largeur de départ identique.
3. Forme spatulée obtenue en détachant le lambeau de la surface intérieure du cylindre lorsque (, voir ci-après). On obtient cette fois des trajectoires divergentes pour les deux fissures conduisant à une longueur de lambeau infinie (en pratique, elle sera égale à la longueur de l’adhésif collé sur le support bien évidemment).
4. Forme elliptique obtenue en détachant le lambeau sur la surface intérieure du cylindre lorsque (, voir ci-après). Bien que nous nous trouvons encore sur la surface intérieure du cylindre, on obtient de nouveau des trajectoires convergentes pour les deux fissures si la largeur initiale du lambeau est inférieure à une certaine largeur critique . Ce comportement est attendu puisque à petite échelle le support semblera plan. Pensez, par exemple, à la courbure de la Terre qui n’est pas significative à petite échelle, comme l’échelle d’un quartier ou d’une ville.

On obtient donc une plus grande variété de formes lorsqu’un support courbe est utilisé. On obtient même des trajectoires divergentes où les deux fissures ne se rejoignent plus.

Théorie : équation des trajectoires

Pour comprendre les formes de lambeau obtenues, il faut observer que le front de décollement est incurvé lorsque le support est courbe. Pour un support plan, ce front est rectiligne et la direction de sa normale coïncide avec la direction de propagation (voir panneau d de la figure ci-dessous). Lorsque le front est incurvé, la normale au front présente un angle avec la direction de propagation. Suivant qu’on se trouve à l’extérieur ou l’intérieur du cylindre qui sert de support pour le film adhésif, cet angle vient s’ajouter ou se soustraire à l’angle que feraient les trajectoires des fissures avec la direction de propagation sur un support plan. Pour chaque position du front de décollement, l’angle que fait la (tangente à la) trajectoire avec la direction de propagation, n’est plus mais

où vaut sur l’extérieur du cylindre et sur l’intérieur de ce dernier. Notez que cette convention de signe pour est arbitraire et que les signes opposés auraient pu être utilisés à condition de changer le signe dans l’expression de .

L’expression de est purement géométrique et est obtenue à l’aide du panneau c de la figure ci-dessus :

Puisque nous connaissons maintenant l’angle que fait la tangente à la trajectoire avec la direction de propagation en tout point, nous pouvons calculer la forme de la trajectoire. En utilisant le système d’axes montré dans la figure ci-dessus, on a, par définition de la tangente, que

En pratique, est toujours bien plus petit que 1 (mesuré en radian); il vaut environ 0.1 en pratique. De plus, on supposera pour simplifier les calculs que , ce qui signifie que la largeur du lambeau sera petite par rapport à la courbure du front de décollement. Dans ces conditions () on a

En utilisant l’expression d’un sinus d’une somme, on obtient

En utilisant le fait que et tels que , et , on obtient finalement l’équation différentielle décrivant la forme des trajectoires

Comme puisque l’axe coupe le lambeau en deux parties égales, on a encore

Notons que si le support est plan, alors et l’équation se réduit à dont la solution, , est l’équation d’une droite formant un angle avec l’axe (si ). On retrouve donc bien une forme triangulaire pour le lambeau.

A ce stade, nous devons encore connaitre la relation existante entre le rayon de courbure du front et le rayon de courbure du support . Cette expression, que nous ne dérivons pas dans cette note mais qui peut être trouvée ici, est

où est l’angle de peeling. Notons que même si le support est courbe, lorsque et l’équation se réduit à celle décrivant les trajectoires sur un support plan. Donc, quand on détache le lambeau avec un angle de peeling de , on obtient de nouveau une forme triangulaire pour le lambeau (voir figure ci-dessous).

Théorie : solution de l’équation

Si on définit les nouvelles variables et , l’équation différentielle décrivant la forme des lambeaux s’écrit alors simplement

La solution générale de cette équation est

où on a utilisé le fait que et où est un point arbitraire le long de la trajectoire (constante d’intégration).

Extérieur du cylindre.

Pour , nous avons des trajectoires convergentes. En effet, pour cette valeur de , la solution est

On constate que quelle que soit la valeur de , le coefficient de l’exponentielle est toujours positif. Le membre de droite de cette équation est donc la différence entre deux nombre positif, le premier variant entre et suivant la valeur de (qui peut être négatif). Il existe donc toujours une valeur de pour laquelle est nulle : . Il s’agit du point où se rencontre les deux trajectoires des fissures. Pour représenter graphiquement cette solution et la comparer aux données expérimentales, on choisira naturellement de placer ce point de rencontre à l’origine des coordonnées. Pour ce faire, on choisit . La solution se réduit donc à

Cette relation est comparée aux données expérimentales dans le panneau supérieur de la figure ci-dessous (attention que par choix du système de coordonnées, les trajectoires se propagent vers les négatifs). L’accord entre la théorie et l’expérience est remarquable.

Intérieur du cylindre.

Pour , nous avons des trajectoires convergentes ou divergente suivant la valeur de , c’est-à-dire suivant la valeur de avec nos nouvelles variables. En effet, pour cette valeur de , la solution est

On constate cette fois que le signe du coefficient de l’exponentielle dépend de la valeur de .

• Lorsque , le membre de droite de cette équation est la somme de deux nombres positifs et ne peut pas s’annuler. Il n’y a donc pas de point de rencontre entre les deux trajectoires; elles sont divergentes. Dans ce cas, il n’y a plus de point remarquable le long des trajectoires et le lambeau sera placé de manière arbitraire le long de l’axe des . On peut par exemple choisir de placer en la partie du lambeau ayant une largeur . Dans ce cas, l’équation décrivant la forme des lambeaux s’écrit

• Lorsque , le premier terme du membre de droite est négatif et varie entre et . Il existe donc toujours une valeur de pour laquelle est nulle : . Il s’agit de nouveau du point où se rencontre les deux trajectoires des fissures. Pour représenter graphiquement cette solution et la comparer aux données expérimentales, on choisira aussi de placer ce point de rencontre à l’origine des coordonnées. Pour ce faire, on choisit . La solution se réduit donc à

Ces deux dernières relations sont comparées aux données expérimentales dans le panneau inférieur de la figure ci-dessous. L’accord entre la théorie et l’expérience est remarquable.

La largeur critique du lambeau séparant ces deux régimes est donnée par

Soit encore en utilisant l’expression de ,

où l’expression de est donnée au début de cette note. Lorsque , les trajectoires sont rectilignes et parallèles. Il s’agit évidemment d’un état instable puisqu’en pratique, il n’est jamais possible de choisir une largeur de lambeau ayant exactement une valeur donnée. La largeur sera soit légèrement supérieure ou inférieure à cette valeur critique.

Comme conclusion relativement anecdotique, on peut dire qu’une pièce avec des murs circulaires est plus simple à détapisser qu’une pièce avec des murs plans puisque dans ce cas nous nous trouvons à l’intérieur d’un cylindre. Si l’on détapisse verticalement (du bas vers le haut par exemple) et que la largeur initiale du lambeau est suffisamment grande, il est alors possible, en théorie, de décoller un lambeau allant du sol au plafond. Notons que la valeur de la largeur critique dépend de l’angle de peeling. Pour obtenir des trajectoires divergentes (et donc une longueur de lambeau illimitée), il faut . Cela se produira d’autant plus facilement que est petit. Il convient donc d’utiliser un angle de peeling petit.

1. O. Kruglova, F. Brau, D. Villers et P. Damman, Phys. Rev. Lett. 107, 164303 (2011)

Les déchirures : I. feuilles adhésives

Support plan

Bien que les papiers peints ne soient plus très à la mode, on s’est tous au moins une fois risqué à détapisser un mur. Pour ce faire, on décolle une partie du papier sur laquelle on tire en espérant détacher un lambeau le plus long possible afin que le travail se termine rapidement. Cependant, on constate très vite combien cette activité est frustrante car bien souvent le lambeau adopte une forme triangulaire au lieu de conserver une forme rectangulaire comme on le souhaiterait. On ne parvient donc pas à retirer en une seule opération autant de papier peint qu’on le voudrait. L’énervement suscité par cet effet pervers nous incite à tirer plus violemment sur les lambeaux mais en vain car la longueur des morceaux n’en est que réduite!

La forme des lambeaux, bien qu’approximativement triangulaire, n’est pas très régulière. Cela provient de plusieurs facteurs. L’adhésion et la vitesse avec laquelle on tire sur le lambeau ne sont généralement pas uniformes. L’angle que fait le lambeau avec le mur varie aussi lors de l’opération. Enfin, une torsion est souvent appliquée au lambeau lors du détachement. Tous ces facteurs influencent la forme des déchirures.

Une expérience un peu plus contrôlée peut facilement être réalisée chez soi à l’aide d’un morceau d’adhésif. Comme illustré sur la figure ci-dessous :

1. Prenez de l’adhésif de 5cm de large et coupez une bande d’une longueur d’environ 15cm. Collez cette dernière sur une table en laissant dépasser 3-4cm d’adhésif.
2. Faites ensuite deux incisions parallèles dans la partie de l’adhésif qui n’adhère pas à la table. Ces incisions se situeront à 0.5cm des bords latéraux et iront du bord libre de l’adhésif jusque la table. La partie non collée de l’adhésif est donc maintenant constituée de 3 languettes : une au centre d’une largeur de 4cm et deux autres externes d’une largeur de 0.5cm.
3. Rabattez les deux languettes externes pour les coller sur la tranche de la table. De cette manière, la seule partie qui n’adhère pas à la table est la languette centrale large de 4cm. Votre dispositif expérimental est maintenant prêt à être utilisé.
4. Tirez doucement sur la languette centrale pour la décoller. De façon à garder un angle constant entre la languette et la table, faites cette opération avec une angle de 180 degrés. C’est-à-dire en rabattant la languette de telle manière que sa face non adhésive soit constamment parallèle avec la table.
5. A mesure que la languette se décolle, vous constaterez que les deux fissures initiées par les deux incisions se rapprochent. La surface de la languette en contact avec la table diminuant au cours du processus, il est donc de plus en plus aisé de la décoller. Afin de garder une vitesse constante pour l’avancée du front de décollement, il convient alors de tirer de moins en moins fort. Quand les deux fissures se sont rejointes, la languette de forme triangulaire se détache de son support.

L’angle que fait chaque fissure avec la direction le long de laquelle on tire est noté (ce qui conduit à un angle au sommet du triangle valant ). L’expression de cet angle en fonction des paramètres du système vaut [1,2]

où est l’épaisseur de l’adhésif (typiquement 50 µm), est l’angle de “peeling” mesuré en radian ( dans cette expérience), c’est-à-dire l’angle avec lequel on détache la languette adhésive, est le module de flexion de la feuille adhésive ( étant le module de Young du matériau composant la feuille), est l’énergie d’adhésion par unité de surface et est l’énergie de fracture par unité de surface.

Plus est grand plus la longueur de la languette détachée sera petite pour une largeur donnée (et plus frustrant sera le détapissage). La relation ci-dessus nous informe que plus l’adhésion est grande plus sera grand, ce qui est assez intuitif. Elle nous informe également que plus l’épaisseur est grande plus sera grand également, ce qui est moins intuitif. Il faut donc éviter de tapisser sur un papier peint déjà posé si on ne veut pas se compliquer la tâche lors d’un détapissage à venir. Finalement, plus le papier peint se déchire facilement (plus est faible) plus sera grand aussi, ce qui est assez intuitif. Il vaut donc mieux utiliser un papier de bonne qualité qui ne se déchirera pas trop aisément.

Un dernier paramètre sur lequel on peut jouer est la vitesse à laquelle on décolle l’adhésif. L’énergie d’adhésion augmente généralement avec cette vitesse et conduit donc à une valeur de plus grande. La figure ci-dessous [1] illustre cette propriété en montrant que la longueur diminue lorsque la vitesse augmente. Il faut donc tirer le plus doucement possible afin de diminuer la valeur de et obtenir des longueurs de lambeau les plus grandes possibles.

Interprétation physique.

On peut comprendre assez facilement l’existence d’un angle optimal apparaissant lors de la déchirure d’une feuille adhésive. L’énergie injectée dans le système provient du travail de la force exercée sur la languette (le lambeau) lorsqu’on tire pour la détacher. Imaginons que la force appliquée sur la languette est initialement nulle et augmente progressivement. Il est clair, après avoir réalisé l’expérience décrite ci-dessus, que si la force exercée est trop faible le front de décollement reste immobile (la languette ne se décolle pas et ne se fissure donc pas non plus). Il existe donc une force minimale à appliquer pour commencer à décoller et fissurer la languette. C’est-à-dire qu’il existe une énergie minimale à injecter dans le système, si on considère un déplacement infinitésimal donné, pour déchirer la languette.

Cette énergie injectée se répartit en énergie de fracture, en énergie d’adhésion, puisqu’il faut fissurer et décoller l’adhésif, mais aussi en énergie élastique puisque la languette est courbée quand on la tire (il y a pli qui relie par la partie collée de l’adhésif à la languette sur laquelle on tire). La somme de ces trois énergies constitue l’énergie totale du système. Pour trouver la trajectoire suivie par chaque fissure, il convient donc de minimiser cette énergie totale. Dès que l’énergie injectée sera égale à ce minimum, le front de décollement pourra avancer suivant l’angle correspondant à ce minimum d’énergie.

Sur le schéma ci-dessous, on constate que :

1. La longueur de la fissure sera la plus courte si celle-ci avance avec un angle représentée par les pointillés rouge. Toute autre trajectoire linéaire possédant un angle conduit à une longueur de fissure plus grande et donc à une énergie plus grande à dépenser. L’énergie de fracture favorise donc un angle nul.
2. La surface décollée, représentée par le trapèze gris, est quant à elle la plus grande possible pour (on a dans ce cas un rectangle). Pour minimiser la surface à décoller, et donc minimiser l’énergie nécessaire pour décoller la languette, il faut au contraire un angle qui tend vers .
3. La courbure du pli est quant à elle constante tout au long du processus mais l’énergie élastique du pli augmente non seulement avec cette courbure (elle augmente comme le carré de celle-ci) mais aussi avec la largeur du pli. Cette largeur diminue d’autant plus vite avec l’avancée du front de décollement que tend vers .

On a donc trois termes énergétiques, dont deux favorisent et un qui favorise . Le système doit donc trouver un compromis afin de qu’aucun des trois termes ne soit complètement défavorisé. Il choisira donc un angle strictement positif mais aussi strictement inférieur à . La valeur précise de cet angle dépend de la pondération de ces trois termes énergétiques [3].

Par exemple, si le matériau composant la languette est très difficile à fissurer ( très grand), et que l’adhésif adhère peu et qu’il se courbe facilement alors l’énergie totale est dominée par l’énergie de fracture. Dans ce cas, minimiser l’énergie totale revient essentiellement à minimiser l’énergie de fracture. Il faut donc que . C’est bien ce que nous dit l’expression de écrite plus haut.

Pour conclure, on constate que l’expression de est indépendante de la largeur . Ce qui signifie que chaque fissure ce propage avec un angle constant jusqu’à ce qu’elles se rejoignent. Elles se propagent donc en ligne droite et dessine un triangle. Même si la valeur de peut varier d’un système à l’autre, suivant les valeurs de paramètres , , et , la forme triangulaire est une caractéristique robuste commune à tous les systèmes. On peut donc se demander s’il n’existe pas un moyen d’influer sur la direction des trajectoires des fissures pour obtenir d’autres figures géométriques. Nous verrons dans un prochain article que si l’adhésif est posé sur un support courbe, les trajectoires ne sont plus rectilignes et qu’elles peuvent même s’éloigner l’une de l’autre.

Pour une vision artistique des choses : Jacques Villeglé.

1. E. Hamm, P. Reis, M. Leblanc, B. Roman et E. Cerda, Nature Mater. 7, 386 (2008)
2. O. Kruglova, F. Brau, D. Villers et P. Damman, Phys. Rev. Lett. 107, 164303 (2011)
3. On retrouve ici un raisonnement similaire à celui rencontré dans l’article sur les structures hiérarchiques de plis dans les rideaux où la longueur de fusion de deux plis était déterminée par deux termes énergétiques, l’un favorisant les grandes valeurs de () et l’autre favorisant les petites valeurs de (). Le système devait alors choisir une valeur de intermédiaire afin de minimiser l’énergie totale égale à la somme de ces deux énergies (voir le graphique suivant).

La hauteur des arbres

Comprendre les formes et structures de la Nature, c’est en grande partie comprendre les échelles de longueur qui les caractérisent. Une échelle de longueur à laquelle on ne prête pas forcément attention, tant elle est banale, est la hauteur des arbres. Certaines essences sont de petite taille, d’autres sont plus grandes. En effet, de nombreuses espèces d’arbres existent, allant des arbustes et arbres fruitiers de nos jardins aux immenses sequoias des parcs américains en passant par les platanes de nos bords de route. Leur taille varie donc du mètre à la centaine de mètres. Le schéma ci-dessous donne quelques ordres de grandeur allant de l’hypérion (l’arbre vivant le plus grand du monde) au pommier en passant par le chêne. Il s’agit de tailles maximales, pour le chêne et le pommier, ou de tailles moyennes pour le Douglas-fir et le Cyprès.

Malgré l’existence d’une grande diversité de plantes, certaines universalités peuvent être mises en évidence par  une analyse minutieuse de leur morphologie et de leur métabolisme [1]. Nous allons montrer ci-dessous que la morphologie des arbres suit un critère assez simple.

Il a été estimé que la taille maximale que peut atteindre un arbre se situe dans l’intervalle 122-130 m [2]. Le transport d’eau jusqu’au sommet de l’arbre est le facteur essentiel qui limite leur taille. Si on ne prend en compte que la résistance mécanique, rien ne limite la taille mais on peut malgré tout obtenir une caractéristique intéressante commune à l’ensemble des arbres.

Intuitivement, pour qu’un arbre soit grand il faut que son tronc soit large. Comme illustré sur la photo ci-dessous [3], si le tronc est trop fin, l’arbre plie sous son propre poids. Même s’il ne se fracture pas, cette morphologie ne lui assure pas les meilleures conditions de développement.

Une idée très simple permet de comprendre, dans une certaine mesure, le lien qui existe entre la hauteur d’un arbre et le diamètre de son tronc. Ce lien induit donc une contrainte universelle sur la morphologie des arbres.

Imaginons, par exemple, une colonne cylindrique faite d’un matériau donné et de diamètre fixé. Il est évident qu’au-delà d’une hauteur critique, la colonne cèdera sous son propre poids. On dit que la colonne flambe comme montré ci-contre (nous avons déjà rencontré ce concept précédemment). A gauche, on voit une colonne intacte alors qu’à droite on distingue la même colonne ayant subi un flambage et qui s’est légèrement affaissée (l’image de droite a été obtenue par une simple déformation numérique de l’image de gauche pour illustrer le propos). Dès qu’un flambage survient, la colonne est structurellement instable et s’effondre rapidement.

On pourrait donc très froidement assimiler un arbre à une colonne cylindrique et chercher quelle est la hauteur maximale que peut atteindre cette colonne, pour un diamètre donné, de manière à ne pas flamber. Evidemment, certains arbres ont une morphologie fortement éloignée d’un simple cylindre. Mais il faut savoir qu’un arbre donné adoptera une forme très différente suivant qu’il est isolé ou qu’il pousse en forêt. Dans une forêt, les autres arbres empêchent la lumière de pénétrer dans le sous-bois et les arbres tendent à ne développer des feuilles (et donc des branches) qu’à leur sommet. Le croquis ci-contre montre la forme d’un chêne isolé (Quercus alba) comparée à la forme d’un chêne poussant en forêt [4]. La photo ci-dessous illustre aussi ce point.

Au lieu de considérer un cylindre, on pourrait bien entendu considérer un cône. Mais les branches du sommet ajoutent une masse supplémentaire qui est, dans une certaine mesure, prise en compte par la simple forme cylindrique. Nous verrons que la limite de stabilité obtenue par l’utilisation d’une colonne cylindrique contraint très bien les mesures effectuées sur le terrain.

En 1881, Greenhill a montré que la hauteur maximale, , que pouvait atteindre une colonne cylindrique de rayon pour qu’elle ne soit pas instable sous son propre poids était [5]

où, est le module de Young du matériau, sa densité et  l’accélération de la pesanteur. Cette relation, et des variantes parfois ad hoc, se retrouve depuis utilisée dans la, très abondante, littérature sur le sujet [3,6]. Notons que le rapport

définit une échelle de longueur caractéristique du problème.

Hormis quelques rares exceptions, le module de Young du bois varie entre 10 et 12 GPa. La densité du bois varie plus significativement entre 500 et 1000 kg/m³ pour la majorité des essences. Nous utiliserons des valeurs moyennes pour l’ensemble des arbres, à savoir 11 GPa pour le module de Young et 750 kg/m³ pour la densité. Il faudrait bien entendu utiliser les valeurs adéquates pour chaque essence, mais nous verrons qu’utiliser ces valeurs approximatives pour l’ensemble des arbres est suffisant pour ce billet. Notons aussi que et apparaissent sous une racine cubique ce qui atténue les erreurs. On obtient donc ( et étant mesuré en mètre)

comme contrainte morphologique associée aux arbres. Autrement dit, pour un diamètre donné, la hauteur des arbres devrait être inférieure à cette hauteur critique si le modèle utilisé n’est pas trop naïf. Le graphique ci-dessous, reprenant environ 5500 points et plusieurs centaines d’espèces d’arbres à travers le monde [6-11], montre en effet que cette contrainte est très bien respectée à quelques rares exceptions près.

Sur ce graphique, le trait continu représente la hauteur critique écrite ci-avant. La zone bleue représente donc la région où un arbre est structurellement stable dans le cadre de ce modèle simplifié. La zone rouge représente la région où un flambage se produit.

On constate donc que non seulement essentiellement tous les arbres se trouvent sous cette limite de flambage mais aussi que le nuage de points est relativement parallèle à cette limite. Cela signifie que la hauteur d’un arbre vaut environ, à une constante près, son diamètre à la puissance 2/3. Le trait discontinu représente le tiers de la hauteur critique. C’est la meilleure courbe de puissance 2/3 passant par ces points. On constate en effet que les points se positionnent uniformément autour de ce trait discontinu (il passe au milieu du nuage de points).

Évidemment, on constate une assez grande dispersion des points conduisant à un nuage assez large et diffus. Il y a au moins deux raisons pour expliquer cette importante dispersion:

1. Chaque essence possède son propre module et sa propre densité . Il faudrait, non pas porter en fonction de en graphique, mais porter en fonction de où est définit plus haut. En effet, la relation de Greenhill, réécrite un peu différemment, nous dit que . Cette courbe ne fait alors intervenir que des nombres (0.788 et 2/3) indépendants du type d’arbre considéré. Les mesures portées ainsi en graphique devraient être un peu moins dispersées. Cependant les données publiées regroupent presque toujours plusieurs espèces d’arbres sur un même graphique représentées par un seul symbole. Il est alors impossible d’extraire les données utiles pour réaliser un tel graphique (sans compter que les modules de Young ne sont pas toujours bien connus). Seuls les spécialistes du sujet possédant les données complètes pourraient effectuer un tel graphique.
2. Même pour une espèce d’arbre donnée, on constate une dispersion significative. En effet, la croissance et le développement d’un arbre sont conditionnés par différents facteurs comme l’accès à l’eau et à la lumière ou l’exposition au vent. Il faudrait donc considérer un ensemble limité d’arbres adultes pour chaque espèce; ces arbres s’étant développés dans des conditions similaires.

1. K.J. Niklas, Plant allometry: the scaling of form and process, University of Chicago Press, 1994
2. G.W. Koch, S.C. Sillett, G.M. Jennings et S.D. Davis, Nature 428, 851 (2004)
3. G. Jaouen et al., Am. J. Bot. 94, 1583 (2007)
4. Croquis par C. Holdrege
5. A.G. Greenhill, Proc. Cambridge Philos. Soc. 4, 65 (1881)
6. USA: T. McMahon, Science 179, 1201 (1973)
7. Canada: S. Huang, S.J. Titus et D.P. Wiens, Can. J. For. Res. 22, 1297 (1992)
8. Australie: M.R. Ngugi et D.B. Botkin, Ecol. Model. 222, 3261 (2011)
9. Amazonie: E.M. Nogueira et al., Forest Ecol. Manag. 255, 2963 (2008); thèse de Nogueira
10. Asie: D.A. King et al., Funct. Ecol. 23, 284 (2009); O.O. Osunkoya et al., Am. J. Bot. 94(12), 1951 (2007)
11. Forêts tropicales: H.C. Muller-Landau et al., Ecol. Lett. 9, 575 (2006)

Plis et Replis: Influence du substrat

Nous avons vu dans le billet précédent que la présence d’un substrat sous une feuille comprimée générait une échelle de longueur intrinsèque indépendante de la taille du système. Nous avons vu que cela était dû à la présence de deux termes énergétiques “antagonistes” présents dans le système; l’un favorise les grandes échelles de longueur (de l’ordre de la taille du système), l’autre favorise les petites échelles de longueur (longueur nulle). Le minimum de l’énergie totale est alors atteint pour une échelle de longueur intermédiaire. Comme tout motif émergent spontanément se caractérise par une (ou plusieurs) échelle de longueur, ce mécanisme constitue un des mécanismes de base de la formation de structure dans un système.

On peut maintenant se demander qu’elle est l’influence de la nature du substrat sur les structures émergentes.

Substrat liquide.

Lorsque le substrat est un liquide, comme de l’eau, la forme adoptée par la feuille mince comprimée est sinusoïdale pour de très petites compressions. La longueur d’onde de cette structure est donnée par

où est la densité du liquide, g est l’accélération de la pesanteur et est le module de flexion de la feuille; E étant le module de Young du matériau composant la feuille et h son épaisseur. On vérifie aisément que le membre de droite de cette relation a bien les unités d’une longueur.

Cette relation nous dit que plus la feuille est rigide (B est grand), plus la longueur d’onde sera grande. En effet, le terme énergétique de déformation de la feuille est celui qui favorise les grandes échelles de longueur. Plus la feuille est rigide plus ce terme domine le système. Par contre, plus le liquide est dense, plus la longueur d’onde est faible. Effectivement, le terme énergétique de déformation du substrat est celui qui favorise les petites échelles de longueur. Plus le liquide est dense plus ce terme domine le système.

Si on utilise une feuille de plastique ordinaire le module de Young sera de l’ordre du GPa (giga Pascal). L’épaisseur typique sera de l’ordre de 20 – 40 µm. Si on utilise de l’eau ( kg/m³) on obtient alors une longueur d’onde de l’ordre de 3 à 5 cm. Si par contre on utilise une feuille de latex (un morceau de gant en latex) le module de Young sera de l’ordre du MPa (mega Pascal). Si on considère la même épaisseur et de l’eau comme substrat, la longueur d’onde est cette fois de l’ordre de 6 à 10 mm.

Lorsque la feuille est comprimée davantage, sa morphologie évolue pour n’obtenir qu’un seul pli qui focalise toute la déformation. La photo ci-contre montre l’évolution de la morphologie en fonction du taux de compression [1]. Pour une compression modeste, la forme est sinusoïdale. Pour une compression un peu plus importante, seules les plis autour du pli central subsistent. Finalement pour une compression de l’ordre de la longueur d’onde apparaissant initialement dans le système, un seul pli subsiste concentrant toute la déformation.

Dans la limite d’une feuille de longueur infinie, une solution exacte décrivant la morphologie de la membrane a été obtenue [2]. Il y a deux familles de solutions énergétiquement équivalentes: l’une symétrique par rapport au milieu de la feuille et l’autre anti-symétrique. Les figures ci-dessous montrent ces solutions (P est relié à la force nécessaire pour comprimer la feuille et est donc relié au taux de compression, et oui cette force diminue à mesure qu’on comprime la feuille).

Substrat élastique.

Lorsque le substrat est un élastomère, un matériau élastique comme le latex ou le caoutchouc, la forme adoptée par la feuille mince comprimée est également sinusoïdale pour de très petites compressions. La longueur d’onde de cette structure est un peu différente comparée au cas précédent et est donnée par

où et sont les modules de Young de la feuille et du substrat respectivement. Si on utilise une feuille de plastique ordinaire d’épaisseur de 20 – 40 µm reposant sur un substrat en latex, la longueur d’onde sera de l’ordre de 1 à 2 mm.

Lorsque la feuille est comprimée davantage, sa morphologie évolue de manière complètement différente comparée au cas où le substrat est un liquide. La structure reste cette fois périodique et les plis formés se séparent en deux familles: l’une voit son amplitude augmenter au détriment de l’autre. Un pli sur deux concentre donc toute l’énergie de déformation pour créer une structure avec une période double de la période initiale. Si on augmente encore la compression, le même processus se répète pour conduire à un quadruplement de la période initiale. La photo ci-contre montre l’évolution de la morphologie en fonction du taux de compression [3].

On constate donc que les morphologies adoptées par une membrane comprimée reposant sur un substrat dépendent fortement de la nature de ce substrat. Ces structures sont donc des signatures claires permettant d’identifier la rhéologie du substrat sans qu’il soit nécessaire d’analyser ce dernier. Cet outil est déjà utilisé, par exemple, dans l’étude des plis géologiques pour déterminer la rhéologie des matériaux au moment de la formation de ces structures.

1. L. Pocivavsek et al., Science 320, 912 (2008)
2. H. Diamant and T.A. Witten, Phys. Rev. Lett. 107, 164302 (2011); Arxiv
3. F. Brau et al., Nature Physics 7, 56 (2011); Arxiv

Plis et Replis: Généralités

Membrane/feuille mince libre

Dans le billet précédent, nous avons évoqué les structures de plis dans les rideaux. Cette structure caractéristique apparaissait car on imposait une déformation particulière en un bord du rideau et, en quelque sorte, ce dernier voulait s’en débarrasser en fusionnant des plis pour atteindre la déformation qui lui coute le moins d’énergie et qui ne comporte ultimement qu’un seul pli.

Si on comprime une feuille de papier en son plan, en la plaçant par exemple sur une table et en essayant de rapprocher deux bords opposés, on atteint directement cette configuration ne comportant qu’un seul pli comme montré sur le photo ci-contre. La feuille ne reste donc pas plane, on dit qu’elle flambe. En effet, il est bien plus aisé de courber une feuille mince que de la comprimer. L’énergie nécessaire pour courber la feuille étant inférieure à celle nécessaire pour la comprimer, le système choisira alors ce mode de déformation. La feuille ne présente qu’une seule ondulation car l’énergie stockée dans une feuille courbée dépend de la courbure au carré. L’énergie sera donc minimale pour une courbure minimale. Comme la feuille ne peut rester plane, elle adoptera une forme courbée ne présentant qu’une seule ondulation sur toute sa longueur (la présence de plusieurs ondulations conduirait à des courbures plus grandes).

Cette morphologie apparait donc en deux temps:

1. La feuille est quelque peu comprimée en son plan avant de flamber (de se courber hors de son plan) car comprimer une feuille mince coute plus cher en énergie que de la courber.
2. Lorsque la feuille a flambé, elle adopte une forme qui minimise son énergie de courbure et ne présente qu’une seule ondulation sur toute sa longueur.

On peut estimer la distance sur laquelle une feuille peut être comprimée avant de flamber. Il suffit pour cela de comparer l’énergie de compression avec l’énergie de courbure en fonction du taux de compression. Lorsque la seconde est plus faible que la première, la feuille flambe. Sans entrer dans les détails ici, on trouve que la distance sur laquelle on peut comprimer une feuille de longueur et d’épaisseur avant d’observer un flambage vaut . Pour une feuille d’une longueur égale à 10cm et d’une épaisseur typique de 100 µm, vaut de l’ordre de 0.1 µm. Inutile de dire que cette compression n’est pas aisément observable.

Membrane/feuille reposant sur un substrat

D’autres morphologies sont pourtant observables quand on comprime une feuille mince. Les structures plissées sont omniprésentes autour de nous. Cela va des plis de la peau aux fruits séchés en passant par les plis géologique, les montagnes, les empreintes digitales, les coulées de lave, etc. Contrairement au cas d’une feuille comprimée, on observe cette fois que la taille des plis (leur longueur d’onde), ne dépend pas de la taille du système. Si le système est plus grand, il y a juste davantage de plis de même taille. Une échelle de longueur intrinsèque caractérise donc ces ondulations. D’où peut-elle provenir?

La différence par rapport au cas d’une simple feuille de papier comprimée est que dans tous ces systèmes la couche mince rigide qui présente ces plis repose cette fois sur un substrat plus épais et plus mou.

L’origine du flambage est toujours la même: il est énergétiquement plus favorable de courber la feuille mince que de la comprimer. Mais quand la feuille flambe, en plus de minimiser sa propre énergie de courbure (qui conduit à une grande ondulation sur toute la longueur de la feuille), le système doit aussi minimiser l’énergie de déformation du substrat qui est solidaire de la feuille et qui se déformera donc avec elle. De manière générale, l’énergie de déformation du substrat favorise les petites ondulations.

On a donc en présence deux termes énergétiques “antagonistes”: l’un favorise des ondulations aussi grandes que possible alors que l’autre favorise des ondulations aussi petite que possible. Pour que tout le monde soit “content”, le système fera un compromis et sélectionnera des ondulations de taille intermédiaire indépendante de la taille du système. Une échelle de longueur intrinsèque au système et qui ne dépend pas des dimensions de ce dernier est donc apparue. La présence de tels termes énergétiques antagonistes dans un système est un des mécanismes de base de la formation de motifs, de structures dans la Nature.