La hauteur des arbres

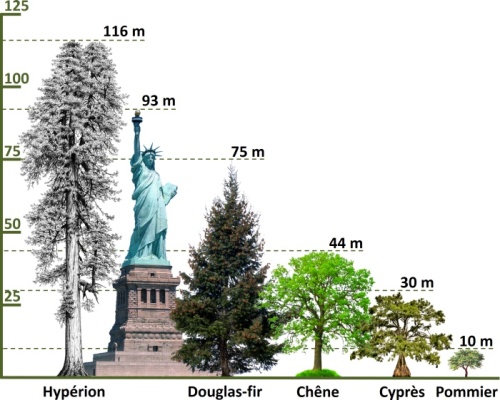
Comprendre les formes et structures de la Nature, c’est en grande partie comprendre les échelles de longueur qui les caractérisent. Une échelle de longueur à laquelle on ne prête pas forcément attention, tant elle est banale, est la hauteur des arbres. Certaines essences sont de petite taille, d’autres sont plus grandes. En effet, de nombreuses espèces d’arbres existent, allant des arbustes et arbres fruitiers de nos jardins aux immenses sequoias des parcs américains en passant par les platanes de nos bords de route. Leur taille varie donc du mètre à la centaine de mètres. Le schéma ci-dessous donne quelques ordres de grandeur allant de l’hypérion (l’arbre vivant le plus grand du monde) au pommier en passant par le chêne. Il s’agit de tailles maximales, pour le chêne et le pommier, ou de tailles moyennes pour le Douglas-fir et le Cyprès.

Malgré l’existence d’une grande diversité de plantes, certaines universalités peuvent être mises en évidence par  une analyse minutieuse de leur morphologie et de leur métabolisme [1]. Nous allons montrer ci-dessous que la morphologie des arbres suit un critère assez simple.

Il a été estimé que la taille maximale que peut atteindre un arbre se situe dans l’intervalle 122-130 m [2]. Le transport d’eau jusqu’au sommet de l’arbre est le facteur essentiel qui limite leur taille. Si on ne prend en compte que la résistance mécanique, rien ne limite la taille mais on peut malgré tout obtenir une caractéristique intéressante commune à l’ensemble des arbres.

Intuitivement, pour qu’un arbre soit grand il faut que son tronc soit large. Comme illustré sur la photo ci-dessous [3], si le tronc est trop fin, l’arbre plie sous son propre poids. Même s’il ne se fracture pas, cette morphologie ne lui assure pas les meilleures conditions de développement.

Une idée très simple permet de comprendre, dans une certaine mesure, le lien qui existe entre la hauteur d’un arbre et le diamètre de son tronc. Ce lien induit donc une contrainte universelle sur la morphologie des arbres.

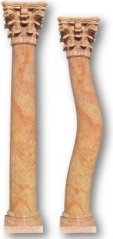Imaginons, par exemple, une colonne cylindrique faite d’un matériau donné et de diamètre fixé. Il est évident qu’au-delà d’une hauteur critique, la colonne cèdera sous son propre poids. On dit que la colonne flambe comme montré ci-contre (nous avons déjà rencontré ce concept précédemment). A gauche, on voit une colonne intacte alors qu’à droite on distingue la même colonne ayant subi un flambage et qui s’est légèrement affaissée (l’image de droite a été obtenue par une simple déformation numérique de l’image de gauche pour illustrer le propos). Dès qu’un flambage survient, la colonne est structurellement instable et s’effondre rapidement.

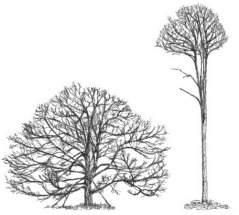On pourrait donc très froidement assimiler un arbre à une colonne cylindrique et chercher quelle est la hauteur maximale que peut atteindre cette colonne, pour un diamètre donné, de manière à ne pas flamber. Evidemment, certains arbres ont une morphologie fortement éloignée d’un simple cylindre. Mais il faut savoir qu’un arbre donné adoptera une forme très différente suivant qu’il est isolé ou qu’il pousse en forêt. Dans une forêt, les autres arbres empêchent la lumière de pénétrer dans le sous-bois et les arbres tendent à ne développer des feuilles (et donc des branches) qu’à leur sommet. Le croquis ci-contre montre la forme d’un chêne isolé (Quercus alba) comparée à la forme d’un chêne poussant en forêt [4]. La photo ci-dessous illustre aussi ce point.

Au lieu de considérer un cylindre, on pourrait bien entendu considérer un cône. Mais les branches du sommet ajoutent une masse supplémentaire qui est, dans une certaine mesure, prise en compte par la simple forme cylindrique. Nous verrons que la limite de stabilité obtenue par l’utilisation d’une colonne cylindrique contraint très bien les mesures effectuées sur le terrain.

En 1881, Greenhill a montré que la hauteur maximale, , que pouvait atteindre une colonne cylindrique de rayon pour qu’elle ne soit pas instable sous son propre poids était [5]

où, est le module de Young du matériau, sa densité et  l’accélération de la pesanteur. Cette relation, et des variantes parfois ad hoc, se retrouve depuis utilisée dans la, très abondante, littérature sur le sujet [3,6]. Notons que le rapport

définit une échelle de longueur caractéristique du problème.

Hormis quelques rares exceptions, le module de Young du bois varie entre 10 et 12 GPa. La densité du bois varie plus significativement entre 500 et 1000 kg/m³ pour la majorité des essences. Nous utiliserons des valeurs moyennes pour l’ensemble des arbres, à savoir 11 GPa pour le module de Young et 750 kg/m³ pour la densité. Il faudrait bien entendu utiliser les valeurs adéquates pour chaque essence, mais nous verrons qu’utiliser ces valeurs approximatives pour l’ensemble des arbres est suffisant pour ce billet. Notons aussi que et apparaissent sous une racine cubique ce qui atténue les erreurs. On obtient donc ( et étant mesuré en mètre)

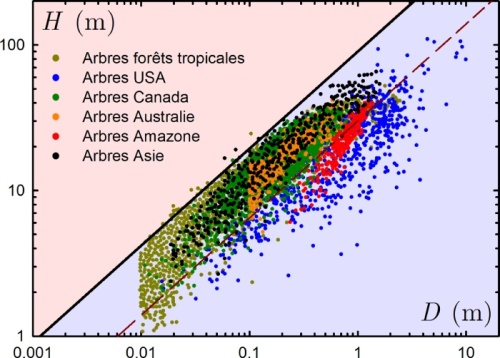
comme contrainte morphologique associée aux arbres. Autrement dit, pour un diamètre donné, la hauteur des arbres devrait être inférieure à cette hauteur critique si le modèle utilisé n’est pas trop naïf. Le graphique ci-dessous, reprenant environ 5500 points et plusieurs centaines d’espèces d’arbres à travers le monde [6-11], montre en effet que cette contrainte est très bien respectée à quelques rares exceptions près.

Sur ce graphique, le trait continu représente la hauteur critique écrite ci-avant. La zone bleue représente donc la région où un arbre est structurellement stable dans le cadre de ce modèle simplifié. La zone rouge représente la région où un flambage se produit.

On constate donc que non seulement essentiellement tous les arbres se trouvent sous cette limite de flambage mais aussi que le nuage de points est relativement parallèle à cette limite. Cela signifie que la hauteur d’un arbre vaut environ, à une constante près, son diamètre à la puissance 2/3. Le trait discontinu représente le tiers de la hauteur critique. C’est la meilleure courbe de puissance 2/3 passant par ces points. On constate en effet que les points se positionnent uniformément autour de ce trait discontinu (il passe au milieu du nuage de points).

Évidemment, on constate une assez grande dispersion des points conduisant à un nuage assez large et diffus. Il y a au moins deux raisons pour expliquer cette importante dispersion:

1. Chaque essence possède son propre module et sa propre densité . Il faudrait, non pas porter en fonction de en graphique, mais porter en fonction de où est définit plus haut. En effet, la relation de Greenhill, réécrite un peu différemment, nous dit que . Cette courbe ne fait alors intervenir que des nombres (0.788 et 2/3) indépendants du type d’arbre considéré. Les mesures portées ainsi en graphique devraient être un peu moins dispersées. Cependant les données publiées regroupent presque toujours plusieurs espèces d’arbres sur un même graphique représentées par un seul symbole. Il est alors impossible d’extraire les données utiles pour réaliser un tel graphique (sans compter que les modules de Young ne sont pas toujours bien connus). Seuls les spécialistes du sujet possédant les données complètes pourraient effectuer un tel graphique.
2. Même pour une espèce d’arbre donnée, on constate une dispersion significative. En effet, la croissance et le développement d’un arbre sont conditionnés par différents facteurs comme l’accès à l’eau et à la lumière ou l’exposition au vent. Il faudrait donc considérer un ensemble limité d’arbres adultes pour chaque espèce; ces arbres s’étant développés dans des conditions similaires.

1. K.J. Niklas, Plant allometry: the scaling of form and process, University of Chicago Press, 1994
2. G.W. Koch, S.C. Sillett, G.M. Jennings et S.D. Davis, Nature 428, 851 (2004)
3. G. Jaouen et al., Am. J. Bot. 94, 1583 (2007)
4. Croquis par C. Holdrege
5. A.G. Greenhill, Proc. Cambridge Philos. Soc. 4, 65 (1881)
6. USA: T. McMahon, Science 179, 1201 (1973)
7. Canada: S. Huang, S.J. Titus et D.P. Wiens, Can. J. For. Res. 22, 1297 (1992)
8. Australie: M.R. Ngugi et D.B. Botkin, Ecol. Model. 222, 3261 (2011)
9. Amazonie: E.M. Nogueira et al., Forest Ecol. Manag. 255, 2963 (2008); thèse de Nogueira
10. Asie: D.A. King et al., Funct. Ecol. 23, 284 (2009); O.O. Osunkoya et al., Am. J. Bot. 94(12), 1951 (2007)
11. Forêts tropicales: H.C. Muller-Landau et al., Ecol. Lett. 9, 575 (2006)